秀英書房

Shuei Shobo

Facebook
X-twitter

MENU

ページの向こうに、
新しい自分がいる。
さあ、まだ誰も知らない、
世界の始まりを覗いてみよう！

New books & Topics

新刊情報

年金だけじゃ生活できない！
「定年バイト」奮戦記

思い出は旋律とともに

『年金だけじゃ生活できない！ 「定年バイト」奮戦記』4月6日発売！

秀英書房 初の電子書籍２点発売開始！　第1弾は平岡正明 著『大山倍達を信じよ』、ノーム・チョムスキー著『言語と認知』

伝説の91歳ピアノ弾き語り ホキ徳田22年ぶりの新刊『思い出は旋律とともに』好評発売中！

『５代将軍「頼嗣」は後鳥羽院の孫なのか』好評発売中！

みんなで楽しむ絵本 『5匹の魔法使いのシーサー』好評発売中！

view more

Web column

ウェブ連載

出版営業K部長のカレー屋探訪記

営業の合間に名店を巡る、カレー愛あふれるK部長の実食レポート。東京を中心に全国のカレー店を訪ね歩き、味や店の雰囲気、人との出会いをスパイシーに綴ります。カレーを通して街と人を味わう、ちょっとディープな食の記録。

writer

キレンジャーの末裔

2026.03.10

17件目 紀伊國屋書店三鷹店（旧啓文堂書店三鷹店）さんに伺ったあとは、無性にカレーが食べたくなります…。

read more
back number

サイエンスナビゲーター® 桜井進の
「素晴らしき数学の世界」

数学の世界を旅する桜井進の連載コラム。数の起源から美しい数式の物語まで、歴史とロマンを交えた知的探訪。日常の中に潜む数学の魅力をひも解きながら、読者をそっと“数の宇宙”へと誘います。

writer

桜井 進

2026.04.06

第2話 メートルの誕生はフランス革命とともに！

read more
back number

Explore books that
inspire you.

書籍一覧を見る

Explore books that
inspire you.

Explore books
that
inspire you.

書籍一覧を見る

Lecture

講演会について

By Professor
Susumu Sakurai

学校教育をもっと楽しく！
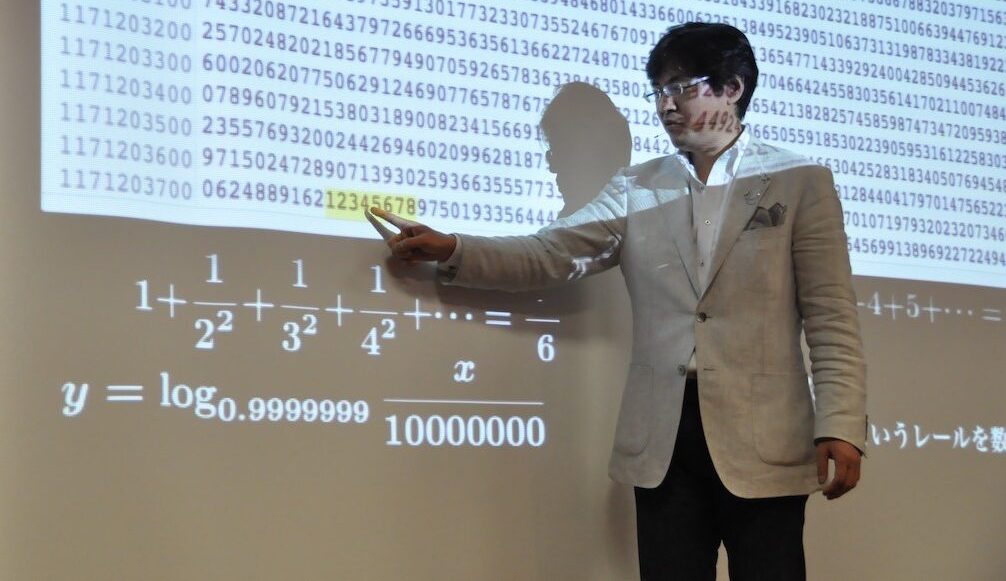
桜井進先生の算数・数学エンタメ講演会

弊社Web連載中のサイエンスナビゲーター®桜井進先生が皆さんの前で映像、音楽を駆使した楽しくて、不思議な算数・数学のエンターテイメント講演会を行います。
桜井先生の著書 『算数なるほど大図鑑 第2版』（ナツメ社刊）の内容をメインに、映像、音楽を駆使したエンターテインメント講演会。他のプログラムも用意しております。
またご希望の講演内容がありましたら、お受けいたします。ぜひ皆さんの学校で開催してみませんか?
view more
 Susumu Sakurai  
 Susumu Sakurai  
 Susumu Sakurai  
 Susumu Sakurai  
 Susumu Sakurai  
 Susumu Sakurai  

カスタム出版

あなたが出版したいジャンルの本、なんでも作成します。
coming soon

書籍・グッズ販売

著者サイン本、弊社オリジナル「書籍×Tシャツ」、
すぐに置きたいブックエンドなど
楽しいグッズ揃えてます！
coming soon

秀英書房

Shuei Shobo

〒156-0051 東京都世田谷区宮坂3-2-10

お問い合わせ

Contact

お問い合わせフォーム
e-mail
tel

©2023 Shuei Shobo All rights reserved.

秀英書房

Shuei Shobo

Facebook
X-twitter
お問い合わせフォーム

2025.09.16

紀伊國屋書店三鷹店（旧啓文堂書店三鷹店）さんに伺ったあとは、
無性にカレーが食べたくなります…。

本日のお昼は、三鷹駅より少し歩いた場所にある Blue Bird さんへ！
お店の外のメニューでドライカレーに即決して入店。
ドライカレーには、ゆで玉子か目玉焼きが付いてきます。
「目玉焼きか？ゆで玉子か？それが問題だ…」ハムレットよろしく悩みたいところでしたが、
ちょうどお昼どき、店内は近くの会社に勤める方々などで満席。
ということで、店員さんに聞かれる前に「ドライカレー、目玉焼きで！」…初来店なのに、
まるで常連のようです。
まずサラダが出てきます。
うお！にんじんドレッシングが超旨い！そしてピクルス&福神漬の入った器が運ばれてきました！

こんなにもらっていいの！？
そしていよいよドライカレーが！
キーマがすごいしっかりしていて、そして半熟の卵の黄身と相まってご飯が
すすむすすむ！堺すすむ（旧い）。
「（ごはん）大盛りにしておけば良かった…」と後悔。（決して量が少ないわけではありません。）
注文の際に常連のフリをした祟りか？
また行きたい！吉祥寺からも行けるので皆様も是非どうぞ！
武蔵野市中町2-16-1 サマリアマンション
1階
map

2026.4.6

第2話 メートルの誕生はフランス革命とともに！

みなさん、こんにちは。サイエンスナビゲーターの桜井進です。
今回は長さの単位から歴史を紐解いてみましょう!

今から約 200 年前のヨーロッパには、長さの単位が 40 万種類以上ありました。さらに、王様が変わるごとに長さの単位を変えることもあり、単位の不統一による混乱は日常茶飯事だったそうです。
では、そもそも長さの単位はどのようにして決められていたのでしょうか。古くは古代オリエントの王様が、肘から中指の先までを“キュービット”としたように、長さの単位の多くは、手足などの体をもとに定められることがほとんどでした。
たとえば、手を広げたときの親指から小指までの幅が“スパン”、親指の幅が“インチ”など。
また、足のつま先からかかとまでの幅を、イギリスでは“フート”、フランスでは“ピエ”と呼んだように、同じ長さでも土地によって単位が異なることもしばしばでした。そして、このような不便さも、当時の人々は「当たり前」と考えていました。

生活の範囲が“ご近所”に限られていた時代は、それでも良かったのかもしれません。しかし、科学や工業が目覚ましい発展を遂げた 18世紀。国際間の交流も盛んになり、単位の不統一は無視できない問題となりました。そこで立ち上がったのが、フランスです。
1790 年、政治家のタレイランの呼びかけを端緒に、私たちが当たり前のように使っている長さの単位、m(メートル)が生み出されたのです。
「北極から赤道までの子午線の、1000 万分の1を基準とする」――これを1mとすることが議会で承認されると、フランスの“地球を測る”一大プロジェクトがスタートしました。
そして 7 年をかけて、同じ子午線上にある、フランス最北端の港町ダンケルクと、スペイン北東部のバルセロナ間、約 1000km の測量に成功します。
時まさにフランス革命の最中。測量隊は苦難の連続だったそうです。
その後、子午線全周の長さが高度な数学によって得られ、“m”が新しい単位として誕生しました。こうした偉業が達成できたのも、フランスが世界有数の数学大国だったから。ちなみに “m”は、フランス語の mètre の頭文字で、「測る」を意味する古代ギリシャ語が語源となっています。

10 進法を用い、これまでにない合理的で便利な単位であったにも関わらず、“m”の普及には時間がかかりました。ですがフランスは熱心に普及に努め、タレイランの呼びかけから実に80年以上のちの1875年、17 か国が署名した“メートル条約”が成立するに至るのです。
条約成立と同時に、白金 90%イリジウム 10%の「メートル原器」がつくられ、1m の基準として使われてきました。その後、より普遍的な基準が求められ、現在では光の速度から、1m は「真空の中で光が 2 億 9979 万 2458 分の 1 秒間に進む距離」と定義されています。
現在、私たちが日常的に使っている“m”には、先人の並々ならぬ努力が込められているのです。
＜著者＞桜井 進 Sakurai Susumu
1968 年山形県生まれ。サイエンスナビゲーター®。
株式会社 sakurAi Science Factory 代表取締役。東京理科大学大学院非常勤講師。
東京工業大学理学部数学科卒、同大学大学院院社会理工学研究科博士課程中退。国土地理院研究評価委員会委員。
在学中から予備校講師として教壇に立ち、数学や物理を楽しく分かりやすく生徒に伝え人気を博す。2000 年にサイエンスナビゲーター®を名乗り、数学における人間ドラマを通して数学の驚きと感動を伝える数学エンターテイメントショーをスタート。全国各地で反響を呼び、多数の学校で講演会を開催中。また多くのメディアに出演、執筆。東京工業大学世界文明センターフェローを経て、現在に至る。
著書・監修本に『雪月花の数学』『感動する！数学』『面白くて眠れなくなる数学』『算数なるほど大図鑑』など100 冊以上、英語・中国語・韓国語に多数翻訳されている。最新刊は『人生は数学でできている』（中公新書ラクレ 刊）
※サイエンスナビゲーターは株式会社 sakurAi Science Factory の登録商標です。
桜井 進