「パパ、マイナス×マイナスがプラスになるのはどうして?」
子どもにたずねられて「そう決まっているの!」とは答えたくないものです。
1+1=2からはじまり分数どうしのわり算まで、小学校の算数は「そういうものだ」という捉え方はけっしてネガティブではありません。もしそれらすべてに生じる「なぜ」にこたえようすれば6年間では済まなくなるからです。
それが“学校の算数”です。できる人(考え抜ける人)を除いて、中学・高校の数学は“学校の数学”です。さて、“学校の算数・数学”を数学として捉えてみます。
「そうきまっているの!」ではないポジティブな答えを目指しましょう。
プラスとマイナスの数
まずは数の正と負についてその意味を考えてみます。0という基準があって0よりも大きい数を正の数、小さい数を負の数と決めることは誰もが納得するところです。
数は正か0か負のどれかです。数直線という図形を用意して、0の位置を決めるとその左側が負、右側が正となります。温度計は上下でその関係になっています。0度より上にいくほど温度が高く、下に行くほど低くなるよう目盛りがふってあります。
 写真:ニセコのスキー場の温度計正負のたし算とひき算
写真:ニセコのスキー場の温度計正負のたし算とひき算さて、正負の足し算と引き算をこの数直線を使って考えてみます。7−3=4は(+7)+(−3)と考えて、「0から右に7だけ進み、次にそこから左に3進むと+4のところに行き着く」と考えることができます。−5+3なら(−5)+(+3)と考えて、「0から左に5だけ進み、次にそこから右に3進むと−2のところに行き着く」という具合です。これらの計算から
正と負というのは向きを表していることがわかります。
 正負のかけ算
正負のかけ算かけ算はこの向きについて考えるのです。(+3)×(+2)=6これは、(+3)×2×(+1)と考えるのです。はじめの(+3)×2は(+3)+(+3)のことですから(+6)になります。それに(+1)を掛けるとはその+6の向きを同じ向きにすること、つまりそのままの+6が答えとなります。
(+3)×(−2)は(+3)×2×(−1)と考えるのです。まず、(+3)×2=+6それに(−1)を掛けるとはその(+6)の向きを反対向きにすること、つまり−6が答えとなります。
「
(−1)を掛けると向きが反対向きになる」と考えるのです。この考え方を、(−3)×(−2)に適用してみます。(−3)×2×(−1)=(−6)これに−1を掛けるとその向きを反対向きにするので+6になるのです。
そもそも(+7)+(−3)の(−3)とは、右に3進もうとするのを逆に左に3進むことを表すことから、(−3)=(+3)×(−1)のマイナス(−1)には逆向きに進ませる働きがあるということです。
マイナス×マイナス=プラスの論理的整合性数学には論理的整合性(logical consistency)があります。あるところで成り立つことは別なところでも成り立たなければなりません。
マイナス×マイナス=プラスの論理的整合性①数と計算の世界には、次のような基本的なルールが見つかります。
〔1のルール〕1×a=a、a×1=a
〔0のルール〕0×a=0、a×0=0、a+(−a)=0、−a+a=0
〔分配法則〕a×(b+c)=a×b+a×cこれらのルールから(−1)×(−1)=1を導くことができます。
1+(−1) =0
(−1)×(1+(−1)) =(−1)×0 両辺に(−1)をかける
(−1)×1+(−1)×(−1)−1+(−1) =0 左辺は〔分配法則〕、右辺は〔0のルール〕
−1+(−1) ×(−1) =0〔1のルール〕から(-1)×1=-1=1
(−1)×(−1)=1〔0のルール〕マイナス×マイナス=プラスの論理的整合性②三角関数の計算の中から(−1)×(−1)=1を導いてみます。
〔2倍角の公式〕cos2θ=(1+cos2θ)/2
(−1)×(−1)=
cos180°×cos180°
=cos2180°
=(1+cos(2×180°))/2
=(1+cos360°)/2=(1+1)/2
=1マイナス×マイナス=プラスの論理的整合性③虚数iはi²=−1という性質をもつ数です。虚数の世界は三角関数と深く結びついています。次はその代表的な公式です。
〔ド・モアブルの公式〕(cosx+isinx)n=cosnx+isinnx
cosπ+isinπ=−1+i×0=−1
なので、
(−1)×(−1)=(cosπ+isinπ)2
=cos2π+isin2π
=1+i×0
=1マイナス×マイナス=プラスの論理的整合性はもっと見つかります。そうなれば、「そうきまっている(−1)×(−1)=1」から「納得する(−1)×(−1)=1」になるでしょう。
桜井進 “X”(旧ツイッター)
https://twitter.com/sakurai_susumu 



 写真:ニセコのスキー場の温度計
写真:ニセコのスキー場の温度計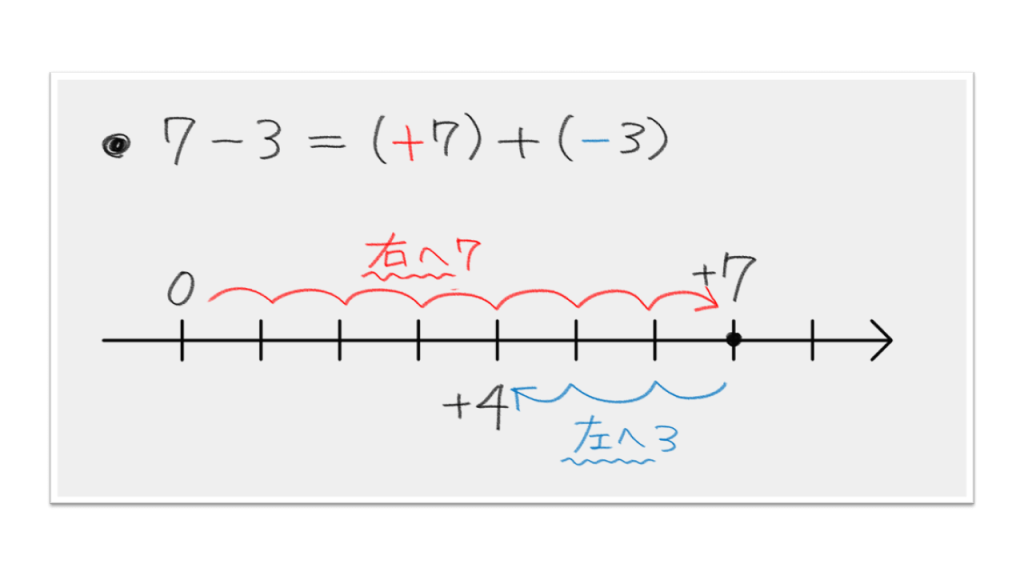 正負のかけ算
正負のかけ算




